Tudomány
A magyar zseni gondolatai ma is új felfedezéseket adnak a világnak

– Decemberben lesz 120 éve, hogy megszületett Neumann János, a számítógép atyja. Ennek alkalmából szeptember 15-én emlékkonferenciát rendeztek a Rényi Intézetben. Miről tanácskoztak?
– Neumann János a 20. század egyik legnagyobb matematikusa volt. Magyarországon kezdte a tanulmányait, a karrierjét, aztán Berlinben és Zürichben szerzett diplomát, majd Amerikába költözött. Hosszú évekig az Institute for Advanced Study professzoraként dolgozott Princetonban, ahol Albert Einstein, Kurt Gödel és más hasonló nagyságok voltak a kollégái. A zseniális magyar tudóst és munkásságát ünnepli 2023-ban a magyar tudományos közélet és a Neumann János Társaság a „Neumann 120” emlékév keretében. Ehhez csatlakozott mind a Magyar Tudományos Akadémia szeptember 14-én egy ülésszakkal, mind a Rényi Intézet a Neumann120 emlékkonferenciával. Mi a matematikai munkásságának néhány aspektusát tekintettük át, különösen azokat, amelyek a tudományos kutatásokra még így, több mint 70 évvel a halála után is nagyon komoly hatásokat gyakorolnak.

– Talán nem túlzás, ha azt mondjuk, hogy ez Neumann János csaknem valamennyi matematikai felfedezésére, illetve gondolatára igaz. Önök melyeket tárgyalták?
– Négy előadást szerveztünk. Ezek közül az elsőt Alain Connes, a Collège de France professzora, szakmánk egyik óriása tartotta, aki Fields-érmet kapott 1982-ben. Hogy kontextusba helyezzem, a Fields Medal a matematikusok legrangosabb díja, amelyet 40 évnél nem idősebb kutatóknak ítélnek oda. A francia tudós egy Neumann által indított kutatási területet, illetve az ő kvantummechanika terén végzett kutatásait fejlesztette olyan magasságba, amiért ezzel a legjelentősebb elismeréssel jutalmazta a matematikus közösség. Az úgynevezett Von Neumann-algebrák reprezentációit vizsgálta, amely még napjainkban is egy aktív és igen fontos terület. Meglepő módon, még a matematikai közéletet is teljesen váratlanul érte, ezek az algebrák egy merőben új területen „bukkantak fel”, vagyis látszólag abszolút össze nem függő területeket kapcsoltak össze. Egy matematikus munkásságának a hatását talán éppen abban lehet a legjobban lemérni, hogy egy felfedezése 40–50 évvel, vagy még később ilyen rendkívüli eredményekhez vezethet. A többi között ezt emelte ki a francia kutató is.

– Számos matematikai eredmény kézzelfogható a mindennapjainkban. Például a számítógép, az okostelefon vagy éppen a numerikus időjárás-előrejelzés, amelyek alapjait Neumann fektette le. Az ön által említett új felfedezés hol jelenik meg az életünkben?
– Erre egyelőre nehéz válaszolni. Kidolgozás alatt állnak ezzel kapcsolatban olyan elméletek, amelyek az orvostudomány egyes problémáinak a megoldásához vihetnek bennünket közelebb, de ezeken még dolgozunk. Ám a többi között éppen az 1930-as években megkezdett kvantummechanikai kutatásnak, illetve a kvantummechanika érthető leírásának köszönhetjük egyebek mellett a nanotechnológiai vívmányokat, köztük a legújabb okostelefonokat. A matematikai eredmények hétköznapjainkban való megjelenésére egyébként Einstein relativitáselmélete a kedvenc példám. Azt gondolnánk, hogy ez egy igen elvont, az életünket abszolút nem befolyásoló felfedezés, mert olyan kis skálán mozgunk, de ez nem igaz. Ahhoz ugyanis, hogy a GPS pontosan megmondja, melyik sávban menjünk, ezeket a relativisztikus egyenleteket kell alkalmaznunk. A matematikai felfedezések tehát mindig visszahatnak az életünkre, csak nem mindig észrevehetőek. Úgy kell ezt elképzelni, mintha lenne egy csomagunk, amelynek csupán a külsejét, a terméket látjuk, de ami benne van, és amitől ez működik, az tipikusan komoly matematikát, elméleti fizikát igényel, és ehhez járult hozzá.

– Melyek voltak a további előadások témái?
– Klaus Schmidt osztrák matematikus, a Bécsi Egyetem nyugalmazott professzora, Matthew D. Foreman, a Kaliforniai Egyetem professzora, végül pedig William Hugh Woodin, a Harvard Egyetem matematikusa absztraktabb témákat tárgyalt. Arról biztosan sokan hallottak már, hogy a matematika axiomatikus felépítésű, vagyis mindig vissza kell mennünk ahhoz a néhány alapvető igazsághoz, következtetési szabályhoz, amelyet korábban a matematikus közösség elfogadott. Neumann sokat dolgozott a jó axiómarendszerek meghatározásán, mivel akkoriban nem volt teljesen egyértelmű, hogy melyek ezek. A matematika legmélyebb alapjait tisztázó tételek, illetve az ezekben végzett munkája tükröződtek vissza ebben a három előadásban.
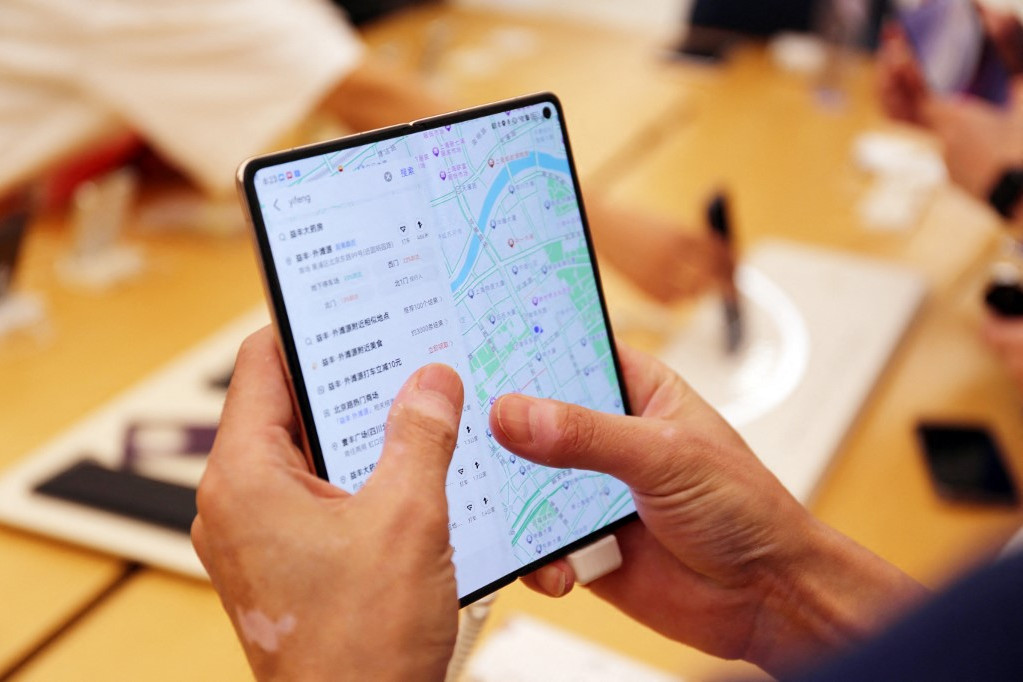
– Miért jelentősek ma is Neumann e területen folytatott kutatásai?
- A matematikai axiómáknak nagyon hosszú történetük van. A tudósok például körülbelül 2000 évig vitatkoztak azon, hogy Eukleidész geometriájának egyes alaptételei kellenek-e vagy sem. Ez vezetett egyébként Bolyai János korszakalkotó geometriai felfedezéséhez, amely ismét eredmények egész hosszú sorát katalizálta, így a már említett Einstein-féle relativitáselmélet matematikájának a kidolgozását is. Ami egyúttal pedig azon módszerre is támaszkodik, amelyet a 19. században dolgoztak ki német matematikusok arra, hogyan lehet jól ábrázolni a teret. És mindennek a vetületét látjuk napjainkban a többi között akkor, amikor a telefonunkon a térképalkalmazást használjuk. Fontosnak tartom, hogy lássuk ezt az ívet, ezáltal pedig azt is, hogy nehéz megítélni egy matematikai eredmény „hasznosságát” a megszületésekor. Évtizedek, nem ritkán évszázadok, sőt évezredek tapasztalata és kutatása áll valamennyi mögött. A zseniális magyar tudós, Neumann János gondolatai tehát ezáltal is folyamatosan új eredményekhez járulnak hozzá, és új felfedezéseket adnak a világnak.